Cluster

Introduction

To reduce both the multiplicative complexity and total number of operations, this paper introduces a modeling scheme of the fast Fourier transform (FFT) to decompose the discrete Fourier transform (DFT) matrix recursively into a set of sparse matrices. We select the Hadamard, modified Haar, and Hybrid (Hadamard-Haar) transforms as examples to show its effectiveness. The proposed scheme significantly reduces the computation complexity and shows better performance than several state-of-the-art FFT methods. To investigate the application of the proposed FFT scheme, we have introduced a multi-stage image encryption algorithm. Experimental comparisons and security analysis have demonstrated the proposed algorithm has good encryption performance and is able to protect different types of images with multiple security levels.

Main results

Image encryption using MSIEA: the top and bottom rows show the encrypted and reconstructed images. (a) grayscale and (b) binary images using Case 1; (c) medical and (d) color images using Case 2.

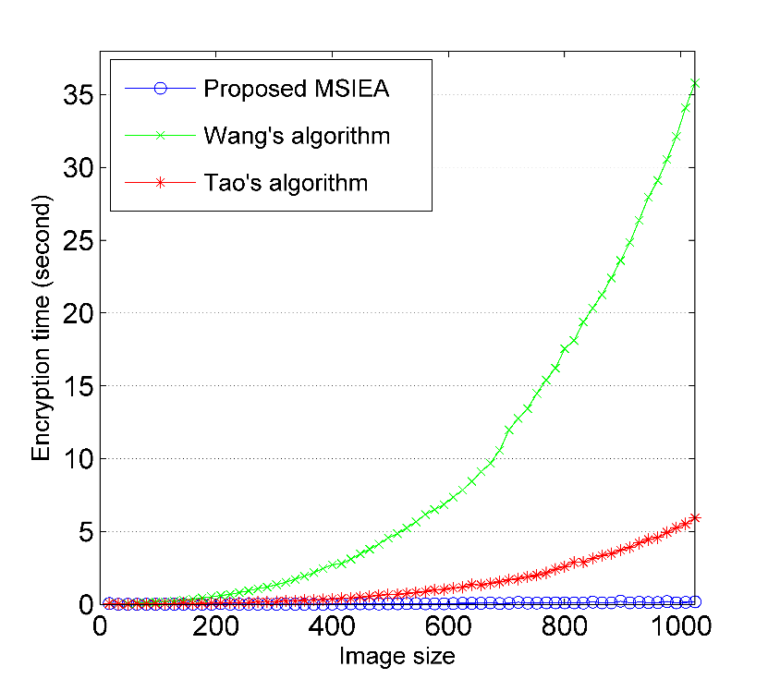Comparison of the computation complexity of different encryption algorithms.

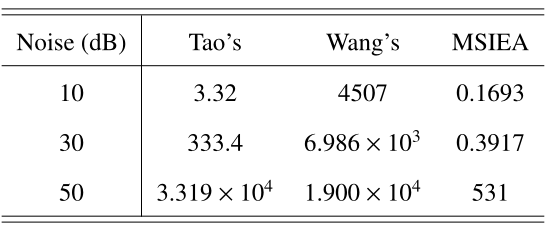MSE results of the images recovered by different algorithms.